Is R2 a Subset of R3

X1 2x2 2. For instance P n the vector space of polynomials of degree less than or equal to n is a subspace of the vector space P n1 of polynomials of degree less than or equal to n 1.

Which Of These Subsets Of R3 Are Subspaces Ie Closed Under Addition And Multiplication Pr 3 1 10 Youtube

In this video we conclude whether the set of all ordered pairs can be regarded as a subspace of the set.

. So in general sloppy language R2 will often be said to be a subspace of R3. A subset of V which is a vector space with the same operations. Another explanation is the vector ab is not the same as the vector ab0.

However R2 is not a subspace of R3 since the elements of R2 have exactly two entries while the elements of R3 have exactly three entries. If W is a subspace then give a geometric description of W. The space R 2 is isomorphic to the subset a b 0 of R 3 but its also isomorphic to infinitely many other 2-dimensional subspaces of R 3.

And in that sense R 2 is clearly a subspace of R 3 as shown above. The action of a linear transformation T. R sorting matrix subset minimum.

That said originally I was a little surprised by the question. Find the subset sorted according to absolute difference between rows in specific columns in a matrix. Advanced Math questions and answers.

Another philosophy is to consider two vector spaces the same if they are the same up to isomorphism that is if they are isomorphic. The de nition of a subspace is a subset Sof some Rn such that whenever u and v are vectors in S so is u v for any two scalars numbers and. It is common to think of R2 as being a subset of R3 using the obvious isomorphism to a subspace of R3.

A mildly canonical one might be to see R2 as all the three-tuples with the third entry zero. Of course R2 can be embedded in many ways in R3. A subset S of Rn is a subspace if and only if it is the span of a set of vectors ie.

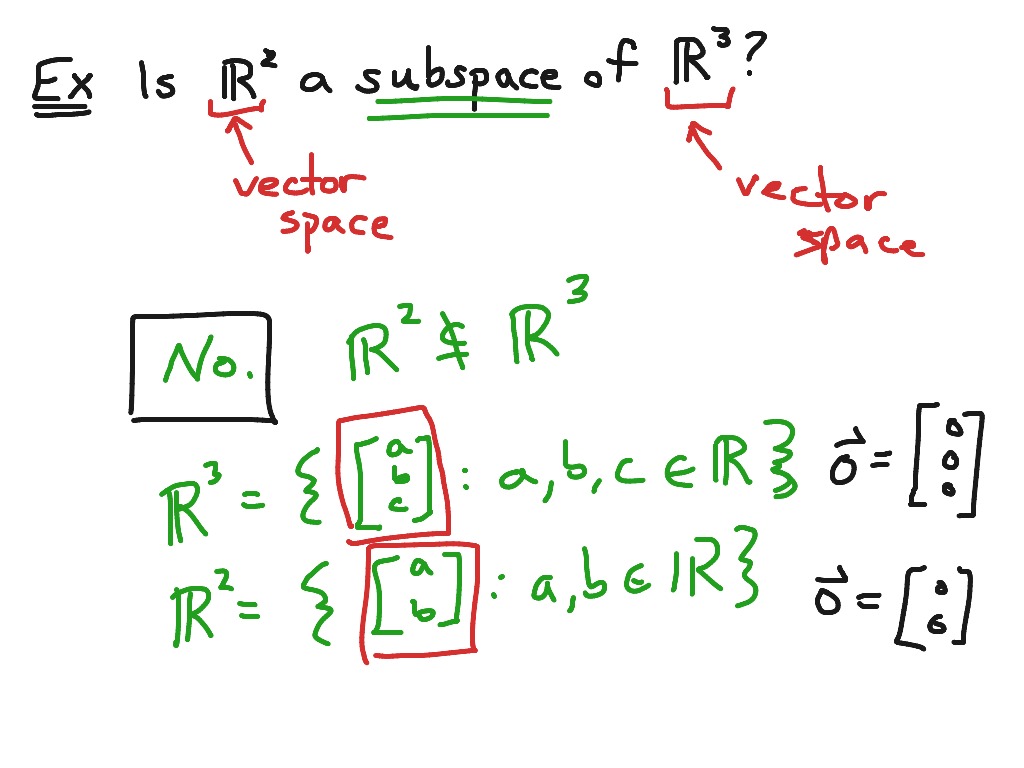
Members of R2 are not members of R3 so R2 is not a subset of R3. Technically no because R2 consists of two-tuples and R3 consists of three-tuples so it is not even a subset. Add to solve later.

Vector spaces are an important algebraic structure. However to identify and picture geometrically subspaces we use the following theorem. Some of them were subspaces of some of the others.

The vector space R2 is not a subspace of R3 because R2 is not even a subset of R3. Determine if the subset of R3 consisting of vectors of the form where abc0 is a subspaceTF This set is a subspace T Determine if the subset of R3 consisting of vectors of the form where abc0 is a subspaceTF The set contains the zero vector. Weve looked at lots of examples of vector spaces.

In that sense R 2 is not a subspace of R 3 as R 2 consists of pairs of real numbers and there are no pairs of real numbers in R 3 only triples. Row r2 to r3 sorted according to increasing difference from row r1 in column c1Any helpclues appreciated. X x y R 2.

Ask Question Asked 8 years 3 months ago. Strictly speaking it is not R2 that is a subspace of R3 it is that subspace. Therefore theres no canonical embedding and you dont usually think of R 2 as being contained in R 3.

A b- a b 0. R 2 R 3 on the basis v 1 v 2 is given by. Find the formula of T x where.

T v 1 2 4 6 and T v 2 0 8 10. In Exercises 917 W is a subset of R3 consisting of vectors of the form X X2 X3 In each case determine whether W is x subspace of R2. The vectors all have three entries whereas the vectors in R2 in R3 have only two The set H s t 0.

4 1 R2 Is Not A Subspace Of R3 Math Showme

Linear Algebra Example Problems Subspace Example 1 Youtube

Solved Prove That The Following Set Is Not A Vector Space Chegg Com